Ouse!
Sempre que se ouve a palavra riscos, imediatamente vem à cabeça dos gestores algo negativo, algo ruim, algo que se deve evitar. Não se deve culpar essas pessoas, até porque o conceito difundido pela principal norma que orienta a gestão de riscos, a ISO 31000, define risco como o “efeito da incerteza nos objetivos”. Por sua vez, os dicionários vinculam o termo “incerteza” a outros termos nada positivos, tais como: “dúvida”, “hesitação” e outros que provocam algum receio.
A notícia boa é que já há algum tempo alguns estudiosos questionam esta relação do risco com incerteza. Ainda lá no ano 1921, Frank Knight, um economista da Universidade de Chicago, observou que a incerteza não apresenta informações mensuráveis que a permitam gerenciar. Nas suas palavras, “risco é tão diferente de uma incerteza não-mensurável, que não se trata, de forma alguma, de uma incerteza”. Evoluindo este pensamento, Aswath Damodaran, professor de finanças da Stern School of Business, na Universidade de Nova York, descreveu, mais recentemente no seu livro Gestão Estratégica do Risco, que risco é “um evento de maior probabilidade, acerca do qual há informações suficientes para avaliar tanto a probabilidade quanto às consequências”. Sendo assim, gestão de riscos não tem nenhuma relação com um “cenário de incertezas”, mas sim com um “cenário de probabilidades”, no qual se tem disponibilidade de dados que permitam estimativas e muitas delas que podem beirar a certeza!
Essa diferença de cenários é corroborada por especialistas em administração de empresas como Anna Moraes que dá uma boa definição dessa relação entre cenários e tomadas de decisão, afirmando que, de uma forma geral, pode-se definir o ato de tomar decisões como fazer escolhas para enfrentar problemas ou aproveitar oportunidades em um continuum que vai do cenário de certeza (altamente previsível) ao cenário de turbulência (altamente imprevisível), sendo que o controle da situação, por parte dos administradores, vai de muito controle à pouco ou nenhum controle entre esses cenários. A figura a seguir ilustra esta relação entre cenários, disponibilidade de informações e controle.
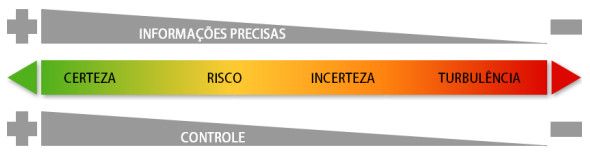
Para ficar mais claro ainda do que é um cenário de risco (ou um cenário de probabilidades), pense em um passageiro que resolve saltar de um avião a dez mil metros de altura sobre a cordilheira dos Andes, sem paraquedas ou nenhum equipamento de segurança. Esse passageiro corre o risco de morrer? A resposta quase automática da maioria das pessoas que recebem esta questão é um retumbante “sim”. No entanto, é seguro afirmar que tal passageiro não corre nenhum risco de morrer. Na verdade, é “certeza” que ele irá morrer! Não há gestão de riscos a fazer nesse caso. Saltou, é morte certa!
Nessa mesma linha de reflexão, podemos perguntar a uma pessoa se existe o risco de cair um meteorito na sua cabeça no mesmo instante em que se faz esta pergunta. Provavelmente a resposta será, também, um convicto “sim”. Todavia, mais uma vez, a resposta está errada, pois nem o melhor astrofísico com os melhores algoritmos, instrumentos e computadores disponíveis conseguiria estimar o ponto exato da Terra onde pode cair um meteorito. Logo isso sim é uma “incerteza”, pois não há dados nem recursos suficientes que permitam calcular tal probabilidade de ocorrência. Nesse caso, ficaria nas mãos de Deus.
Peter Bernstein, que escreveu “A Fascinante História do Risco”, declara que sem números e nem probabilidades, o único meio de lidar com o risco é apelar para os deuses e o destino.
Por outro lado, temos, felizmente, essa relação de riscos com a disponibilidade de números, dados e probabilidades mensuráveis e calculáveis, tornando viável lidar com eles e fazer a gestão de riscos, pois, no cenário de probabilidades, podemos aplicar o mais poderoso dos instrumentos à nossa disposição: a Matemática (e tudo que deriva dela). Inclusive podemos aplicá-la não só para nos proteger do mal como também para capturar oportunidades a nosso favor! Afinal de contas, a gestão de riscos deve ser aplicada para evitar a Lei de Murphy – que alerta que sempre algo pode dar errado – e executar a Lei de Gérson, que prega “tirar vantagem em tudo”, mas aqui, vamos considerar apenas no sentido ético, é claro!
Por falar em obter vantagens, muito antes de toda essa discussão conceitual sobre riscos, lá nos idos anos 1500, um matemático renascentista chamado Girolamo Cardano, considerado por muitos o pai da teoria da probabilidade, já havia capturado a ideia da relação de riscos com probabilidades. Então, inveterado em apostas, ele decidiu pensar nos riscos de forma positiva, focar em probabilidades favoráveis e partiu para os jogos de dados. Mas antes de saber o que Cardano observou, responda este desafio:
Num jogo de par de dados que você deve acertar a soma das duas faces que caem para cima, qual a soma entre 2 a 12 você escolheria para vencer o adversário?
Responda antes de continuar a leitura.
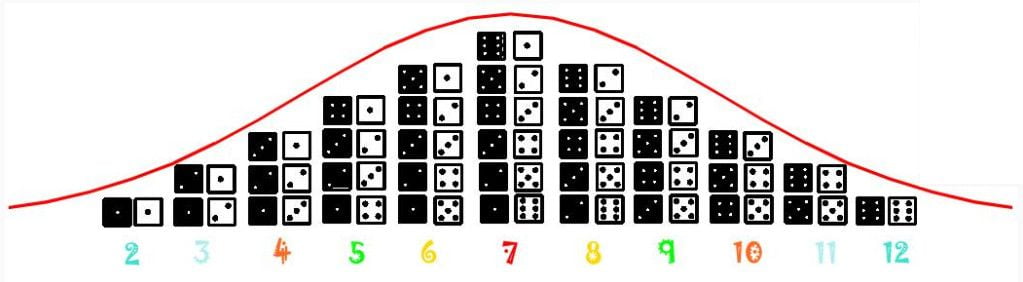
Observe a importância das combinações no cálculo das probabilidades envolvendo o jogo de par de dados. Há seis combinações possíveis para se obter o número 7 na jogada de um par de dados. Isso representa cinco vezes mais chances de ganhar escolhendo o número 7 do que escolhendo os números 2 ou 12, que seriam as piores escolhas, pois só há uma combinação possível para cada uma dessas duas somas. Logo, a melhor escolha para o jogo de par de dados é o número 7. As chances aumentam muito mais se a aposta envolver muitas jogadas. Probabilidade tem uma relação estreita com frequência. A frequência de jogadas implica diretamente nas probabilidades do resultado. Sendo assim, é recomendável apostar em resultados consolidados não de uma, duas ou três jogadas, mas sim na maior quantidade possível. As probabilidades apontam que em cem jogadas, é muito provável que em 16 ou 17 delas (16,66%), dará o número 7, um percentual maior que as demais possibilidades. As outras combinações não alcançarão este percentual, tornando o jogador conhecedor dessa informação, um vencedor!
Perceba que a distribuição das combinações dos dados forma uma curva típica. Curvas desse tipo são chamadas “distribuição normal” ou “curva do sino” e compreendem um fenômeno que vem sendo notado desde 1733, quando foi revelado pela primeira vez pelo matemático francês Abraham de Moivre. Desde então a curva do sino vem sendo referência para identificar padrões que dão origem a retorno de eventos e pode auxiliar em previsões e decisões com bastante assertividade. A distribuição normal é um fenômeno observado na distribuição de altura, peso ou idade de uma população, dentre outros aspectos da natureza.
Fenômeno semelhante à Distribuição Normal, temos o Princípio de Pareto, formalizado no século XIX por Vilfredo Pareto, um economista italiano que desenvolveu métodos para estudar e descrever a distribuição desigual das riquezas no país, quando observou que 80% das riquezas produzidas estava nas mãos de 20% da população. Essa relação 80/20 vem sendo percebida em vários outros cenários: 80% dos crimes são cometidos por 20% dos criminosos, 80% dos acidentes de trânsito são causados por 20% dos motoristas, 20% dos seus produtos representam 80% das vendas, 20% dos empregados são responsáveis por 80% dos resultados, 80% da poluição têm origem em 20% das fábricas, 20% dos alunos têm as notas 80% mais altas, 20% dos posts geram 80% do tráfego, etc. Considerar fenômenos como estes é obter dados e parâmetros muito significativos para lidar com riscos.
Mas retomando a questão da influência da frequência nas probabilidades, isso fica mais claro ao analisarmos outro fenômeno chamado Paradoxo do Aniversário, apresentado pela primeira vez pelo matemático polonês Richard von Mises. Tal como Will Smith e Margot Robbie, no filme Golpe Duplo, dirija-se a um estádio de futebol e desafie alguém a apostar que dentre todas as 23 pessoas em campo (22 jogadores mais o juiz), duas delas fazem aniversário numa mesma data. A probabilidade de você estar certo é de 50%. Grandes chances de ganhar a aposta! Mas se você não estiver seguro, inclua na conta os jogadores reserva para alcançar a quantidade de 30 pessoas. Com essa quantidade a probabilidade de acerto aumenta para 70%. Se ainda assim não estiver seguro, acrescente os bandeirinhas e os gandulas até ter um número de 57 pessoas, daí pode apostar com máxima segurança de vitória, pois a probabilidade de acerto vai para mais de 99%. Percentual nesse nível é legalmente aceito até para confirmar paternidade (veja teste de DNA)! Lembre-se: lidar com risco não é uma relação determinística, mas sim probabilística. Ainda assim, pode ser muito favorável e até aceito como “certeza”.
A teoria das probabilidades não para por aí em apoiar a gestão de riscos positivos. Imagine que um apresentador de um programa de auditório te orienta a escolher uma dentre três portas, sendo que atrás de uma delas há, ocultamente, um Camaro e atrás das outras duas há bodes. Você se posiciona em frente a uma das portas na tentativa de acertar aquela que tem o carro. Daí o apresentador abre uma das outras duas portas não escolhidas por você e mostra que lá há um bode. Depois ele pergunta se você quer mudar de porta, escolhendo a outra porta que ainda está fechada. Você mudaria de porta? As recomendações probabilísticas apoiadas no teorema de Bayes, elaborado pelo matemático inglês Thomas Bayes nos anos 1700, dizem que você terá dois terços de chances se trocar de porta contra um terço de chances se continuar na porta escolhida inicialmente. Portanto, matematicamente, é recomendável que você troque de porta. Este é conhecido como o problema do Paradoxo de Monty Hall. Monty Hall de fato foi o apresentador de um programa de game show chamado Let’s Make a Deal, na TV americana dos anos 1960 e de fato realizava desafios como este no seu programa.
E matemática tem muito mais a oferecer em possibilidades de gerenciamento de riscos. Veja a sequência de Fibonacci, que é uma sucessão de números descrita no século XII pelo matemático italiano Leonardo de Pisa, mais conhecido como Fibonacci. O matemático percebeu uma regularidade matemática representada em vários aspectos da natureza, como em caracóis e flores de girassóis. Estudiosos observam que esse fenômeno parece remeter a um melhor aproveitamento natural do espaço na acomodação dessas composições na Natureza. Mas o fato é que a sequência de Fibonacci levou à “Proporção Áurea” ou o “Número de Ouro”, percebido por diversos observadores como referências de beleza em obras de arte de Leonardo da Vinci, músicas de compositores clássicos, literatura, arquitetura das pirâmides do Egito e outras ocorrências consideradas praticamente “divinas”. Além de todas essas aplicações, investidores do mercado de ações observaram que a flutuação do mercado financeiro na bolsa de valores obedece a um padrão relacionado com a sequência de Fibonacci, tanto que softwares de investimentos incluem um módulo denominado Fibonacci. Investidores garantem que o uso desse módulo costuma ser bastante assertivo nas operações na bolsa.
Tal como aos investidores da bolsa, probabilidades assertivas sustentam todas as empresas de seguro do mundo. Ou alguém acredita que elas existiriam se as probabilidades de sinistro fossem desfavoráveis a elas? Essas empresas tem todos os dados a sua disposição: idade, sexo, moradia, qualidade do bem segurado, histórico de sinistros, padrão de comportamento, etc. Daí é só jogar na fórmula e calcular o seguro com base no percentual de risco resultante. Numa relação de perdas e ganhos, elas só existem por os ganhos serem certamente maiores! A vida é mais gerenciar riscos do que poder contar com certezas para se apoiar, e é disso que as empresas de seguro vivem.
Há, também, diversas outras histórias reais em que a teoria das probabilidades foi aplicada com a intenção de capturar oportunidades a obter vantagens sobre o que se denomina “riscos positivos”. O filme O Homem que Mudou o Jogo, estrelado por Brad Pitt, conta uma delas que ocorreu com o time de baseball Oakland Athletics na temporada de jogos do ano de 2002. O Oakland A’s era praticamente um time falido, sem grande orçamento para contratar jogadores caros em destaque. Então a direção do time foi ampliada com a participação de Peter Brand, um economista formado em Yale que veio para implementar um novo sistema de análise e recrutamento de jogadores baseando-se em estatísticas sobre seus desempenhos históricos individuais. Jogadores sem expressividade, mas friamente analisados e combinados, foram colocados em campo. O resultado foi que o Oakland quebrou um recorde que durava cem anos e que ainda não foi superado nos dias de hoje! O time venceu vinte partidas consecutivas. Embora, por motivos adversos, não tenha vencido a temporada, seu método foi adotado pelo rival Red Sox, que se tornou vencedor em 2004, título que não alcançava desde 1918.
As melhores histórias de riscos positivos são contadas no livro A Sabedoria das Multidões, de James Surowiecki. Há a história do submarino americano Scorpion que, em maio de 1968, desapareceu em seu caminho de volta para Newport News depois de uma viagem de serviço no Atlântico Norte. Embora a marinha soubesse a última localização informada do submarino, não tinha ideia do que acontecera e nem vaga ideia do quão longe ele poderia ter viajado após ter feito contato pelo rádio. Então o oficial John Craven formou um grupo com alguns homens de conhecimentos distintos, incluindo matemáticos, especialistas em submarinos e homens de resgate, e pediu-lhes palpites sobre possíveis cenários de causas do desaparecimento do submarino. Craven cruzou os palpites, aplicou, também, o teorema de Bayes e chegou a uma estimativa do ponto em que o submarino estava. Cinco meses após o desaparecimento, um navio da marinha encontrou o Scorpion. Em uma extensa área marítima possível, o submarino estava a apenas 220 metros de onde o grupo de Craven havia dito que estaria.
O passeio do cientista Francis Galton em uma feira agropecuária em Plymouth, Inglaterra em 1906 também é uma boa história do livro de Surowiecki. No passeio, Galton se deparou com uma gincana. Quem acertasse o peso de um boi, após abatido e tratado, receberia um prêmio. Oitocentas pessoas escreveram seus nomes e palpites em pedaços de papel e arriscaram a sorte. Ao final do evento e entrega do prêmio ao vencedor, Galton, matemático que era, pediu, ao organizador do evento, os papéis com os palpites para realizar um estudo. Ele calculou a média dos oitocentos palpites. O cálculo de Galton mostrou que a multidão reunida estimou que o boi pesaria 1.197 libras (0,54 t), o que era apenas uma libra a menos do que foi de fato o peso do boi tratado. Isso é menos de 500 gramas de diferença sobre um boi que pesava mais de meia tonelada!
Histórias como a de Galton e a do submarino Scorpion são provas de que o autor Barry Libert faz a afirmação correta no próprio título do seu livro: “Nós Somos Mais Inteligentes do que Eu”. Portanto, “nós” formamos a sabedoria das multidões.
O canal History Channel apresentou, recentemente em um dos seus programas, um experimento semelhante ao de Galton. O cientista do programa colocou sobre uma mesa em uma praça um pote de jujubas e pediu às pessoas que passavam que dessem um palpite de quantas jujubas havia no pote. Mesmo com uma frequência muito baixa de apenas 24 palpites, o cientista calculou a média desses palpites e observou que a sabedoria das multidões estimou o conteúdo do pote com apenas uma jujuba a menos do volume real.
Em uma live realizada no dia 17 de novembro de 2021, o Instituto Modal também quis reproduzir a “brincadeira” e repetiu o experimento. Na live Gestão de Riscos em Projetos Ágeis, apenas 19 participantes sugeriram um palpite. O pote do Modal continha 250 jujubas e a média dos palpites dos internautas apontou uma estimativa de 272. Certamente um pouco mais de palpites (frequência), aproximaria mais a estimativa do resultado real. Entretanto a brincadeira foi apenas uma dinâmica de envolvimento, pois o objetivo principal da live fora demonstrar que a sabedoria de uma multidão, no caso a multidão de signatários do Manifesto Ágil, iniciado no ano 2001, incluindo Kent Beck, criador do método ágil denominado Extreme Programming (XP) e Ken Schwaber e Jeff Sutherland, criadores do método Scrum, revolucionou a maneira de conduzir projetos de desenvolvimento de software no mundo. A dissertação de mestrado de um dos participantes da live, o qual escreve este artigo, reuniu informações que justificam tal conclusão, incluindo uma pesquisa envolvendo oito órgãos do governo brasileiro. A pesquisa, que contou com a orientação de doutores da Universidade de Brasília, concluiu ser seguramente positivo arriscar utilizar métodos ágeis no desenvolvimento de software para o governo em detrimento dos métodos tradicionais extremamente rígidos, burocráticos, morosos, mais custosos e complexos. O The Standish Group, uma organização que avalia desempenho de projetos de software há quase 20 anos, publicou que os métodos ágeis têm uma taxa de sucesso mais de três vezes maior que os métodos tradicionais. Com os métodos ágeis corre-se altos riscos positivos de economicidade, eficiência, eficácia e maximização do atendimento do interesse público (efetividade).
É importante lembrar que o que fazemos no Governo e para o Governo vai para a sociedade, logo volta para nós mesmos, volta para os nossos filhos, parentes e amigos, volta para as pessoas que amamos! Por isso é tão importante fazer bem feito!
A palavra risco vem do italiano “riscare” que quer dizer “ousar”! Se há informações suficientes para avaliar tanto a probabilidade quanto as consequências, e se as estimativas são favoráveis, ouse!
